[BZOJ] 1075 最优驾车drive [SCOI2007]
Description
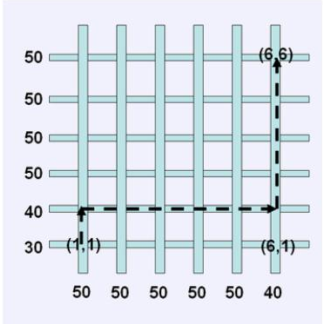
有$$n$$条南北方向的双向街道和$$n$$条东西方向的双向街道纵横交错。相邻街道(不管是哪个走向)的距离均为$$L$$英
里。西南角交叉口的坐标为$$(1,1)$$,东北角为$$(n,n)$$。在所有交叉口均可任意改变行驶方向。每条街道有它自己的最
高速度限制,该限制对整条街道有效(不管行驶方向如何)。你的任务是从交叉口$$(x_s,y_s)$$开车行驶到$$(x_t,y_t)$$,要
求只能在交叉口处改变速度,行驶过程中不得违反所在街道的速度限制,只能沿着路程最短的线路行驶,并且行驶
时间在给定的闭区间$$[t_1,t_2]$$内。车速以“每小时英里数”为单位,它必须是5的正整数倍。若车速为$$v$$,则每加仑
汽油能行驶的英里数为$$80-0.03v^2$$。
Input
输入第一行为两个整数$$n, L$$, 第二行包含$$n$$个正整数,从南到北描述$$n$$条东西走向的街道的速度限制,第三行包
含$$n$$个正整数,从西到东描述$$n$$条南北走向的街道的速度限制。第四行包含六个正整数$$x_s, y_s, x_t, y_t, t_1, t_2$$.
Output
如果无解,输出No,否则输出两行,分别描述最早到达的方案(若有多种方案,选择其中最省油的)和最省油
的方案(如果有多种方案,选择其中最早到达的)。每种方案用两个数表示,第一个数表示到达时刻(单位:分钟
,向上取整);第二个数表示耗油量(单位:加仑,四舍五入保留两位小数)。
Sample Input
样例输入1
6 20
30 40 50 50 50 50
50 50 50 50 50 40
1 1 6 6 300 320
样例输入2
8 2
10 20 20 30 10 20 10 10
10 20 20 30 10 20 10 20
6 8 2 4 10 39
Sample Output
样例输出1
300 6.25
318 5.60
样例输出2
No
样例说明
样例1的最快路线为以40英里/小时为速度匀速前进,路程为200英里,因此时间为5小时,每加仑 汽油可以行驶$$80-0.03 \times 40 \times 40=32$$英里,因此耗油量为$$\frac{200}{32}=6.25$$加仑。最省油路线是先以40英里/小时行驶120英 里,然后以35英里/小时行驶80英里,耗油量为$$120 \div 32+80 \div (80-0.03 \times 35 \times 35)=5.60$$加仑。下图的路线可以同时满足 两种方案(其中第二种方案需要在$$(6,2)$$处改变速度)。
限制
100%的数据满足:$$1 \leq n \leq 10, 1 \leq l \leq 20, 0 \leq t_1 \leq t_2 \leq 1000$$. 速度限制不超过50
思路
由于本题只能沿着路程最短的线路行驶,意味着$$x$$和$$y$$方向,都只能朝着一个确定的方向走,而且不能走出起点和终点形成的矩形,很容易发现这是一个 DP 的模型,我们记录$$dp[i][j][t]$$为$$x$$方向走了$$i$$步,$$y$$方向走了$$j$$步,且目前所花的时间为$$t$$的最小耗油是多少。这个 DP 是很容易通过刷表来转移的(枚举下一步的方向以及速度),但是有一个巨大的问题:
如果我们的速度是$$v$$,那么走$$l$$的耗油是$$\frac l {80 - 0.03v^2}$$L,花的时间是$$\frac l v$$,耗油以及时间都是实数,但它们中至少有一个得做状态,怎么办呢?
考虑将时间转换,虽然速度不同,所花的时间就不同,但不同的速度所花的时间却是成比例的,换句话说,我们可以用一种“代价”来替换时间,只需满足比例相同,就可以达到同样的效果。由于速度是55的整数倍,所以我们先将速度除以5,对应的时间整体增加了5倍,这样速度就只有1, 2, 3, 4, 5, 6, 7, 8, 9, 10这几个值,我们不妨求出他们的$$\mathrm{lcm} = 2520$$,令速度$$v$$的代价$$\mathrm{cost}_v = \frac {\mathrm{lcm}} i$$,这样代价均是整数,而且代价与时间对应成比例,不难发现,如果代价和是$$s$$,那么对应的时间(分钟)为:
$$ \frac {s}{\mathrm{lcm}} \cdot L \cdot 60 \cdot \frac {1}{ 5}
$$
总的代价和不会超过$$2 \cdot n \cdot \mathrm{lcm}$$所以复杂度为:$$O(n^3\mathrm{lcm}\cdot 20)$$.
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int ReadInt() {
static int n, ch;
n = 0, ch = getchar();
while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) n = (n << 3) + (n << 1) + ch - '0', ch = getchar();
return n;
}
const int MAX_N = 10 + 2, MAX_V = 50;
const int LCM = 2520, MAX_COST = LCM * 2 * MAX_N;
const double INF = 1e50, eps = 1e-8;
int n, lim_x[MAX_N], lim_y[MAX_N], time_cost[MAX_V], L;
double dp[MAX_N][MAX_N][MAX_COST];
inline double cal(int v) {
return (double)L / (80 - 0.03 * v * v);
}
inline void tension(double &a, const double &b) {
if (b < a) a = b;
}
inline int dcmp(const double &a) {
return fabs(a) < eps ? 0 : (a < 0 ? -1 : 1);
}
void solve() {
int x1 = ReadInt() - 1, y1 = ReadInt() - 1, x2 = ReadInt() - 1, y2 = ReadInt() - 1, t1 = ReadInt(), t2 = ReadInt();
int dx = x2 - x1 > 0 ? 1 : -1, dy = y2 - y1 > 0 ? 1 : -1;
int delta_x = abs(x1 - x2), delta_y = abs(y1 - y2);
dp[0][0][0] = 0;
for (int i = 0; i <= delta_x; ++i)
for (int j = 0; j <= delta_y; ++j)
for (int t = 0; t < MAX_COST; ++t) if (dp[i][j][t] != INF) {
static int x, y, rx, ry;
x = i + 1, y = j;
if (x <= delta_x) {
ry = y1 + y * dy;
for (int v = 1; v * 5 <= lim_x[ry] && t + time_cost[v] < MAX_COST; ++v)
tension(dp[x][y][t + time_cost[v]], dp[i][j][t] + cal(v * 5));
}
x = i, y = j + 1;
if (y <= delta_y) {
rx = x1 + x * dx;
for (int v = 1; v * 5 <= lim_y[rx] && t + time_cost[v] < MAX_COST; ++v)
tension(dp[x][y][t + time_cost[v]], dp[i][j][t] + cal(v * 5));
}
}
int min_time = -1, min_oil = -1;
for (int t = 0; t < MAX_COST; ++t) if (dp[delta_x][delta_y][t] != INF) {
double ti = (double)t * L / LCM * 12;
if (dcmp(ti - t1) >= 0 && dcmp(t2 - ti) >= 0) {
if (min_time == -1) min_time = t;
if (min_oil == -1) min_oil = t;
else if (dcmp(dp[delta_x][delta_y][t] - dp[delta_x][delta_y][min_oil]) == -1) min_oil = t;
}
}
if (min_time == -1) return puts("No"), void();
printf("%d %.2lf\n", (int)ceil((double)min_time * L / LCM * 12), dp[delta_x][delta_y][min_time]);
printf("%d %.2lf\n", (int)ceil((double)min_oil * L / LCM * 12), dp[delta_x][delta_y][min_oil]);
}
int main() {
n = ReadInt(), L = ReadInt();
for (int i = 0; i < n; ++i) lim_x[i] = ReadInt();
for (int i = 0; i < n; ++i) lim_y[i] = ReadInt();
for (int i = 1; i <= MAX_V / 5; ++i) time_cost[i] = LCM / i;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
for (int t = 0; t < MAX_COST; ++t)
dp[i][j][t] = INF;
solve();
return 0;
}