[计蒜客]蒜头君的树

题目描述

蒜头君有一棵有根树，树的每一边都有边权，蒜头君想知道任意两点间最短距离之和为多少。另外，由于各种原因，蒜头君的树的边的边权会发生若干次改变，蒜头君想让你告诉他，每一次改变后，任意两点间最短距离之和为多少？

输入格式

第一行一个正整数n，表示蒜头君的树上的结点个数。

接下来n-1行，每行两个正整数$$x_i,y_i$$$$x_i$$​​表示$$i+1$$结点的父亲结点的编号，保证其父结点编号小于自己编号。$$y_i$$​​表示$$i+1$$号结点的父亲结点与自己间边的距离。

接下来一行一个整数m，表示树的边权发生改变的次数。

接下来m行，每行两个正整数a,b表示将a结点与其父亲结点之间的距离改为b，保证$$a \geq 2$$。

输出格式

先输出一个整数，表示对于原始的树任意两点间最短距离之和。

接下来m行，每行输出一个整数，表示每一次改变后，任意两点间最短距离之和。

数据规模

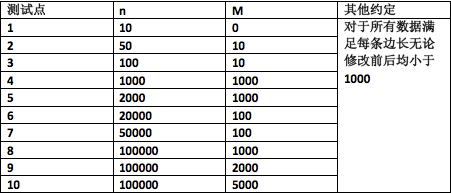
样例输入

4
1 1
1 1
1 1
1
2 2

样例输出

9
12

思路

dfs

$$最短距离和= \sum（树上每一条边被最短路经过的次数 \times 这条边的长度）$$

$$一个节点到它父节点的边被经过的次数=该节点以及它的子孙的节点个数 \times 除了该节点和它子孙之外的所有节点总个数$$

每一个节点以及它子孙节点的个数总和用一遍dfs保存在num数组中，然后$$ans+= num[i] \cdot (n - num[i])$$，就可以求出在没有进行任何操作时的最短距离和。

对于每一次操作将第x个节点到它父节点的边长由原来的a[x]改为y，则将原来的最短距离和$$ans+=(y-a[x])(num[x])(n-num[x])$$，同时将a[x]改为y即可。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int MAXNUM=1e6+10;
ll a[MAXNUM];
ll n,m;
ll num[MAXNUM];
vector<int>E[MAXNUM];

void dfs(int x)
{
    num[x]=1;
    for(int i=0;i<E[x].size();i++)
    {
        int v=E[x][i];
        dfs(v);
        num[x]+=num[v];
    }
}

ll read()
{
    ll ans=0,f=1;
    char i=getchar();
    while(i<'0'||i>'9'){if(i=='-')f=-1;i=getchar();}
    while(i>='0'&&i<='9'){ans=ans*10+i-'0';i=getchar();}
    return ans*f;
}

int main()
{
    n=read();
    for(int i=2;i<=n;i++)
    {
        int x;
        x=read();a[i]=read();
        E[x].push_back(i);
    }
    dfs(1);
    ll ans=0;
    for(int i=2;i<=n;i++)
    {
        ans+=a[i]*(ll)(num[i])*(ll)(n-num[i]);
    }
    printf("%lld\n",ans);
    m=read();
    while(m--)
    {
        ll x=read(),y=read();
        ans+=(y-a[x])*(ll)(num[x])*(ll)(n-num[x]);
        printf("%lld\n",ans);
        a[x]=y;
    }
}