[计蒜客]A.蒜头君打地鼠

题目

问题描述

蒜头君最近迷上了打地鼠，但他发现同时出现在面板上的地鼠太多，于是他想改进一下他的锤子，于是他拿出了一款

$$k \times k$$大小的正方形锤子，但是遗憾的是，这个锤子只能斜着砸。如下图所示：

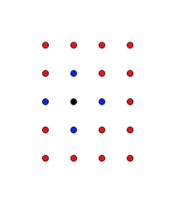
当k=2时，若蒜头君敲击黑点，黑点和图中所有蓝色点将一并被敲到。

当k=3时，锤子的图案如下所示

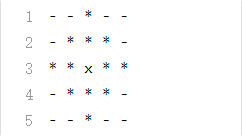
k取其他值时以此类推。

注意：蒜头君只能敲击面板上的格子，但锤子不一定要全部落在面板内。

现在给定一个$$n \times n$$的面板，每个格子可能有地鼠也可能没有地鼠，请编程计算用$$k \times k$$大小锤子敲击时最多能打中多少地鼠。

输入格式

第一行2个整数n,k，表示面板大小和锤子大小。

接下来n行，每行n个整数，若为1代表该格子有地鼠，若为0代表该格子无地鼠。不会出现其他的数字。

输出格式

输出一个整数，代表最多能砸到的地鼠数。

对于50% 的测试数据，满足$$1 \leq n \leq 300 , 1 \leq k \leq 10 $$;

对于80% 的测试数据，满足$$1 \leq n \leq 2000,1 \leq k \leq 10$$;

对于100% 的测试数据，满足$$1 \leq n \leq 2000,1 \leq k \leq 100$$.

样例说明

敲击第2行的0，可以敲到周围的4个地鼠。

样例输入

样例输出

思路

将原矩阵顺时针旋转45°，二维前缀和预处理，然后枚举每一个可能砸到的正方形之和并取最大。

枚举的正方形的四个顶点必须是从原矩阵璇转过来的点，用vis数组判断。

代码

#include <iostream>
#include <stdio.h>
#include <string.h>
#define MAX_N 4005
using namespace std;

int n,k,t;
int ans;
int a[MAX_N][MAX_N];
int sum[MAX_N][MAX_N];
bool vis[MAX_N][MAX_N];

void read()
{
    memset(a,0,sizeof(a));
    memset(vis,false,sizeof(vis));
    scanf("%d%d",&n,&k);
    t=n;
    int temp;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            scanf("%d",&temp);
            a[i+j][n-1-i+j]=temp;
            vis[i+j][n-1-i+j]=true;
        }
    }
    n=n*2-1;
    k=k*2-1;
}

bool is_legal(int x,int y)
{
    return x+y>=t-1 && n-1-x+y>=t-1 && n-1-y+x>=t-1 && 2*n-2-x-y>=t-1 && vis[x][y];
}

void cal_sum()
{
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            if(i-1>=0) sum[i][j]+=sum[i-1][j];
            if(j-1>=0) sum[i][j]+=sum[i][j-1];
            if(i-1>=0 && j-1>=0) sum[i][j]-=sum[i-1][j-1];
            sum[i][j]+=a[i][j];
        }
    }
}

int cal_max()
{
    int maxn=0;
    for(int i=0;i<n && i+k-1<n;i++)
    {
        for(int j=0;j<n && j+k-1<n;j++)
        {
            if(!is_legal(i,j) || !is_legal(i,j+k-1) || !is_legal(i+k-1,j) || !is_legal(i+k-1,j+k-1)) continue;
            int now=sum[i+k-1][j+k-1];
            if(i-1>=0) now-=sum[i-1][j+k-1];
            if(j-1>=0) now-=sum[i+k-1][j-1];
            if(i-1>=0 && j-1>=0) now+=sum[i-1][j-1];
            maxn=max(maxn,now);
        }
    }
    return maxn;
}

void solve()
{
    cal_sum();
    ans=cal_max();
}

void print()
{
    printf("%d\n",ans);
}

int main()
{
    read();
    solve();
    print();
}

[计蒜客] 蒜头君打地鼠(2017NOIP 提高组模拟赛1,Day1,A)