[洛谷]平衡点 [JSOI]
题目描述
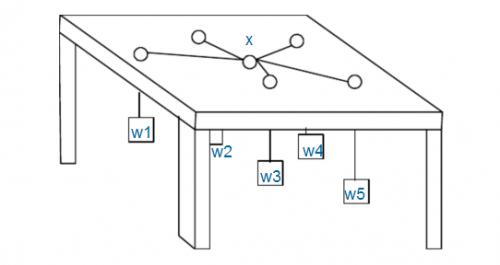
如图:有n个重物,每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞,然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的(不会造成能量损失),桌子足够高(因而重物不会垂到地上),且忽略所有的摩擦。
问绳结X最终平衡于何处。
注意:桌面上的洞都比绳结X小得多,所以即使某个重物特别重,绳结X也不可能穿过桌面上的洞掉下来,最多是卡在某个洞口处。
输入输出格式
输入格式:
文件的第一行为一个正整数n(1≤n≤1000),表示重物和洞的数目。接下来的n行,每行是3个整数:Xi.Yi.Wi,分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )
输出格式:
你的程序必须输出两个浮点数(保留小数点后三位),分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。
输入输出样例
输入样例
30 0 10 2 11 1 1
输出样例
0.577 1.000
思路
搜索,将每个力正交分解
我们可以确定一个原点,将所有的力在这个原点上正交分解,最终我们可以得到所有的力的一个合力,而真正的平衡点一定在合力所指向的方向
每当分解得到一个合力之后,将原点在合力的方向上位移一定的距离。每当原点位移的方向发生了改变的,缩小以后操作的位移距离。
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef double db;
const db esp = 1e-5;
const int maxn = 1000 + 10;
int n;
struct node { int x, y, w; };
node pos[maxn];
struct Node { db x, y; };
Node now;
int dx = 1, dy = 1;//移动方向1+ 0-
void dfs(db delta)
{
db x = 0, y = 0;
db len = 0;
for (int i = 1; i <= n; i++)
{
len = sqrt((now.x - pos[i].x) * (now.x - pos[i].x) + (now.y - pos[i].y) * (now.y - pos[i].y));
if (!len) continue;
//将(x,y)正交分解
x += pos[i].w / len * (pos[i].x - now.x);
y += pos[i].w / len * (pos[i].y - now.y);
}
len = sqrt(x*x + y*y);
now.x += delta / len*x;
now.y += delta / len*y;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d%d%d", &pos[i].x, &pos[i].y, &pos[i].w);
db move = 5000;//移动的步长
Node pst;//移动前的位置
while (1)
{
pst.x = now.x; pst.y = now.y;
dfs(move);//移动点
if (abs(pst.x - now.x) <= esp && abs(pst.y - now.y) <= esp)
{
break;
}
if ((dx != (now.x > pst.x)) || (dy != (now.y > pst.y)))
{
dx = !now.x > pst.x;
dy = !now.x > pst.y;
move = move*0.8;//缩小
}
}
printf("%.3lf %.3lf\n", now.x, now.y);
}